Analytic Continuation Over the Punctured Unit Disk

Analytic Continuation
Analytic continuation (sometimes called simply "continuation") provides a way of extending the domain over which a complex function is defined. The most common application is to a complex analytic function determined near a point by a power series
 | (1) |
Such a power series expansion is in general valid only within its radius of convergence. However, under fortunate circumstances (that are very fortunately also rather common!), the function will have a power series expansion that is valid within a larger-than-expected radius of convergence, and this power series can be used to define the function outside its original domain of definition. This allows, for example, the natural extension of the definition trigonometric, exponential, logarithmic, power, and hyperbolic functions from the real line
to the entire complex plane
. Similarly, analytic continuation can be used to extend the values of an analytic function across a branch cut in the complex plane.
Let and
be analytic functions on domains
and
, respectively, and suppose that the intersection
is not empty and that
on
. Then
is called an analytic continuation of
to
, and vice versa (Flanigan 1983, p. 234). Moreover, if it exists, the analytic continuation of
to
is unique.
This uniqueness of analytic continuation is a rather amazing and extremely powerful statement. It says in effect that knowing the value of a complex function in some finite complex domain uniquely determines the value of the function at every other point.
By means of analytic continuation, starting from a representation of a function by any one power series, any number of other power series can be found which together define the value of the function at all points of the domain. Furthermore, any point can be reached from a point without passing through a singularity of the function, and the aggregate of all the power series thus obtained constitutes the analytic expression of the function (Whittaker and Watson 1990, p. 97).
Analytic continuation can lead to some interesting phenomenon such as multivalued functions. For example, consider analytic continuation of the square root function . Although this function is not globally well-defined (since every nonzero number has two square roots),
has a well-defined Taylor series around
,
which can be used to extend the domain over which is defined. Note that when
, the power series for
has a radius of convergence of 1.
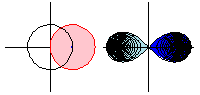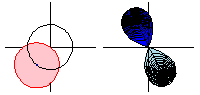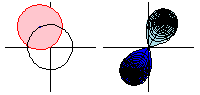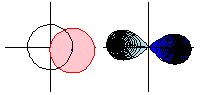
The animation above shows the analytic continuation of along the path
. Note that when the function goes all the way around,
is the negative of the original function, so going around twice returns the function to its original value.
In the animation, the domain space (colored pink; left figures) is mapped to the image space (colored blue; right figures) by the square root function, and the light blue region indicates the negative square root. However, by continuing the function around the circle, the square root function takes values in what used to be the light blue region, so the roles of the blue and light blue region are reversed.
This can be interpreted as going from one branch of the multivalued square root function to the other. This illustrates that analytic continuation extends a function using the nearby values that provide the information on the power series.
It is possible for the function to never return to the same value. For example, increases by
every time it is continued around zero. The natural domain of a function is the maximal chain of domains on which a function can be analytically continued to a single-valued function. For
, it is the connected infinite cover of the punctured plane, and for
it is the connected double cover. If there is a boundary across which the function cannot be extended, then is called the natural boundary. For instance, there exists a meromorphic function
in the unit disk where every point on the unit circle is a limit point of the set of poles. Then the circle is a natural boundary for
.
See also
Analytic Function, Branch Cut, Branch Point, Continuity Principle, Direct Analytic Continuation, Global Analytic Continuation, Monodromy Theorem, Multivalued Function, Natural Boundary, Permanence of Algebraic Form, Schwarz Reflection Principle Explore this topic in the MathWorld classroom
Explore with Wolfram|Alpha
References
Arfken, G. Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press, pp. 378-380, 1985. Davis, P. J. and Pollak, H. "On the Analytic Continuation of Mapping Functions." Trans. Amer. Math. Soc. 87, 198-225, 1958. Flanigan, F. J. Complex Variables: Harmonic and Analytic Functions. New York: Dover, 1983. Havil, J. "Analytic Continuation." §16.3 in Gamma: Exploring Euler's Constant. Princeton, NJ: Princeton University Press, pp. 91-193, 2003. Knopp, K. "Analytic Continuation and Complete Definition of Analytic Functions." Ch. 8 in Theory of Functions Parts I and II, Two Volumes Bound as One, Part I. New York: Dover, pp. 83-111, 1996. Krantz, S. G. "Uniqueness of Analytic Continuation" and "Analytic Continuation." §3.2.3 and Ch. 10 in Handbook of Complex Variables. Boston, MA: Birkhäuser, pp. 38-39 and 123-141, 1999. Levinson, N. and Raymond, R. Complex Variables. New York: McGraw-Hill, pp. 398-402, 1970. Morse, P. M. and Feshbach, H. Methods of Theoretical Physics, Part I. New York: McGraw-Hill, pp. 389-390 and 392-398, 1953. Needham, T. "Analytic Continuation." §5.XI in Visual Complex Analysis. New York: Clarendon Press, pp. 247-257, 2000. Rudin, W. Real and Complex Analysis. New York: McGraw-Hill, pp. 319-327, 1987. Whittaker, E. T. and Watson, G. N. "The Process of Continuation." §5.5 in A Course in Modern Analysis, 4th ed. Cambridge, England: Cambridge University Press, pp. 96-98, 1990.
Referenced on Wolfram|Alpha
Analytic Continuation
Cite this as:
Weisstein, Eric W. "Analytic Continuation." From MathWorld--A Wolfram Web Resource. https://mathworld.wolfram.com/AnalyticContinuation.html
Subject classifications
Source: https://mathworld.wolfram.com/AnalyticContinuation.html
0 Response to "Analytic Continuation Over the Punctured Unit Disk"
Post a Comment